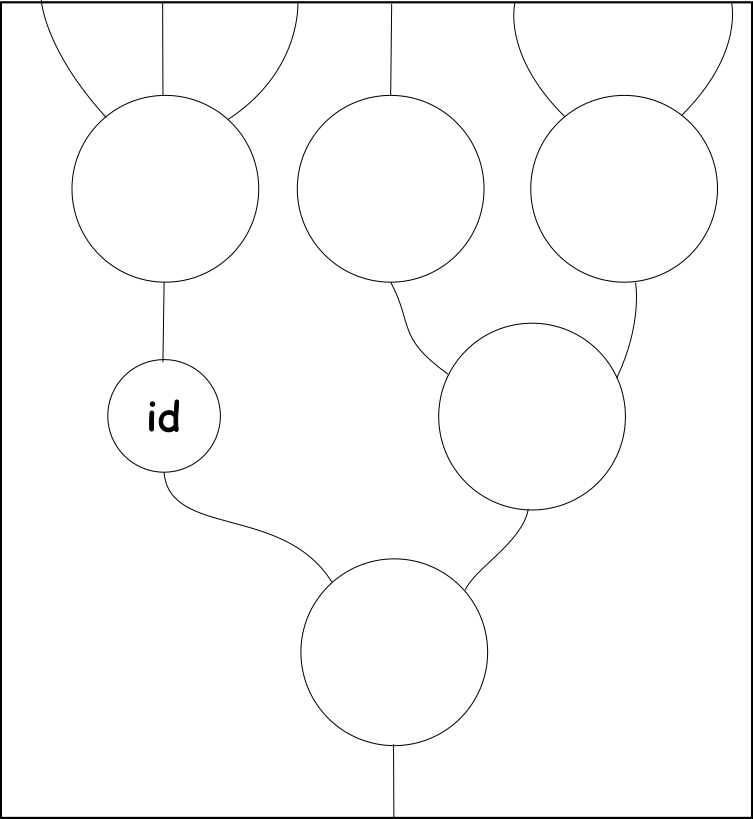
I’ve been thinking a bit about interpolation recently. In animation programming, we often use interpolation as a way to ensure continuity when transitioning from one animation to another. The most basic type of interpolation is linear interpolation, given by
$$
a +_s b = sa + (1-s)b\,,
$$
for vectors \(a, b\) and weight \(s\). Another common type is spherical interpolation, where we interpolate between two rotations (represented as unit quaternions) along a shared great circle in the \(3\)-sphere.
This got me thinking – can we axiomatize the common properties of different interpolation operators? Let \(+_t\) be a family of binary operators on some set \(A\), indexed by \([0, 1]\). What properties might we ask such a family of operators to satisfy in order to qualify as a form of interpolation? We can ask for a kind of commutativity:
$$a +_t b = b +_{1-t} a\,.
$$
If we work hard enough, we can also ask for a kind of associativity:
$$
(a +_s b) +_t c = a +_{st} (b +_{\frac{t-st}{1-st}}c)\,,
$$
if \(s\) and \(t\) are not both \(1\), and
$$
(a +_1 b) +_1 c = a +_1 ( b +_t c )
$$
for any \(t\).
We might also want a kind of idempotence:
$$
a +_t a = a\,,
$$
and special behaviour for the endpoints \(1\) and \(0\):
$$
a +_0 b = a\,.
$$
These raise a few questions.
- Is there a name for these algebraic structures?
- Does this generalize to an algebraic theory that works in categories other than the category of sets? (For example, monoids can be defined in any monoidal category, commutative monoids in any symmetric monoidal category, and groups in any Cartesian category.)
- In what sense is it correct to use the words ‘associativity’, ‘commutativity’ and ‘idempotence’ to refer to these rules as we have done?
- If we have a rule for associativity, why isn’t there a rule for an identity element?
- Is there a neater presentation (particularly with regards to the associativity rule)?
Let’s start with associativity. A monoid is a set \(M\) together with an associative binary operator \(M \times M \to M\) that has an identity element. But there’s an alternative definition of monoid that I quite like. For this definition, instead of defining a single binary operation, we instead ask that \(M\) should be equipped with an \(n\)-ary operator \(\_*\cdots*\_ \colon M^n \to M\) for each \(n = 0, 1, \cdots\). Furthermore, we ask that these operations should be compatible in the following sense, which can be thought of as a generalized associativity rule.
$$
( a_{1,1} * \cdots * a_{1,k_1} ) * \cdots * ( a_{n,1} * \cdots * a_{n,k_n} ) = a_{1,1} * \cdots * a_{1,k_1} * \cdots * a_{n,1} * \cdots * a_{n,k_n}
$$
This is the same as a monoid, because if we have the binary operation \(\_*\_\), then we can construct the \(n\)-ary operation (for \(n\ge2\)) by repeated application; associativity then tells us precisely that the \(n\)-ary operation so constructed is well-defined: it does not depend on the order in which we chain together the binary operation.
The existence and defining property of the identity element is the \(0\)-ary part of this definition: the \(0\)-ary operation \(1 \to M\) picks out an element \(e\) (thought of as an empty product), and then the above rule tells us that for any \(x\), we must have
$$
e * x = x\,,
$$
taking \(n = 2\), \(k_1=0\), \(k_2 = 1\) and \(a_{1,1}=x\) (and, similarly, that \(x * e = x\)).
Let’s now turn to our interpolation theory. If we start with our binary operations \(+_s\) and apply them repeatedly, what are the \(n\)-ary operations that we’re expecting to get out? A little thought reveals that \(n\)-ary operations should correspond to sequences \(s_1,\cdots,s_n\) of non-negative real numbers that sum to \(1\). Given such a sequence, we write the corresponding operation as $$ s_1a_1 + \cdots + s_na_n\,, $$ where our original \(a +_s b\) would now be written as \(sa + (1 – s)b\). This is still an abstract \(n\)-ary operator – we don’t have a concept of addition and multiplication.
The corresponding generalized associativity rule is as follows. $$ s_1 ( t_{1,1}a_{1,1} + \cdots + t_{1,k_1}a_{1,k_1} ) + \cdots + s_n ( t_{n,1}a_{n,1} + \cdots + t_{n,k_n}a_{n,k_n} ) = s_1t_{1,1}\,a_{1,1} + \cdots + s_1t_{1,k_1}\,a_{1,k_1} + \cdots + s_nt_{n,1}\,a_{n,1} + \cdots + s_nt_{n,k_n}\,a_{n,k_n}\,.
$$
This also answers our question about why there is no identity rule in our theory. There is no \(0\)-length list of non-negative real numbers that sums to \(1\).
Enter operads
The last section revealed a nice little structure on the collection of lists of non-negative real numbers that sum to \(1\). Given natural numbers \(n, k_1,\cdots,k_n\) and sequences of non-negative real numbers
$$
s_1,\cdots s_n\,, \
t_{1,1},\cdots,t_{1,k_1}\,,
\cdots\,,
t_{n,1},\cdots,t_{n,k_n}\,,
$$
each summing to \(1\), we can form a new list of length \(k_1 + \cdots + k_n\), also summing to \(1\), given by
$$
s_1t_{1,1}, \cdots, s_1t_{1,k_1}, \cdots, s_nt_{n,1}, \cdots, s_nt_{n,k_n}\,.
$$
Moreover, this ‘composition’ operation satisfies a natural kind of associativity: if we write \(C(n)\) for the set of all sequences \(s_1,\cdots,s_n\) that sum to \(1\), then the following diagram commutes.
$$
\require{AMScd} \begin{CD} \prod_{i=1}^n\prod_{j=1}^{k_i}C(l_{i,j}) \times \prod_{i=1}^n C(k_i) \times C(n) @>>> \prod_{i=1}^n\prod_{j=1}^{k_i}C(l_{i,j})\times C\left(\sum k_i\right)\\ @VVV @VVV \\ \prod_{i=1}^n C\left(\sum_{j=1}^{k_i}l_{i,j}\right) \times C(n) @>>> C\left(\sum_{i=1}^n\sum_{j=1}^{k_i}l_{i,j}\right) \end{CD} $$
Lastly, there is a ‘unit’ for the composition operation: the \(1\)-element sequence \(1\). Indeed, if we write our composition operator as \((\_;\cdots;\_)\circ\_\), then we have
\begin{align}
(s_1,\cdots,s_n)\circ 1 &= s_1,\cdots,s_n\,;\\
(1;\cdots;1)\circ(s_1,\cdots,s_n) &= s_1,\cdots,s_n\,,
\end{align}
for all sequences \(s_1,\cdots,s_n\in C(n)\).
If you find the diagrams and equations above confusing, then I recommend sitting down and trying to write down the natural definitions that come to mind. You should end up with something similar.
Is there a name for this kind of structure? Yes! It’s called an operad. As the name suggests, it helps very much to think of the elements of \(C(n)\) as being like \(n\)-ary operations: functions that take \(n\) inputs and have one output.

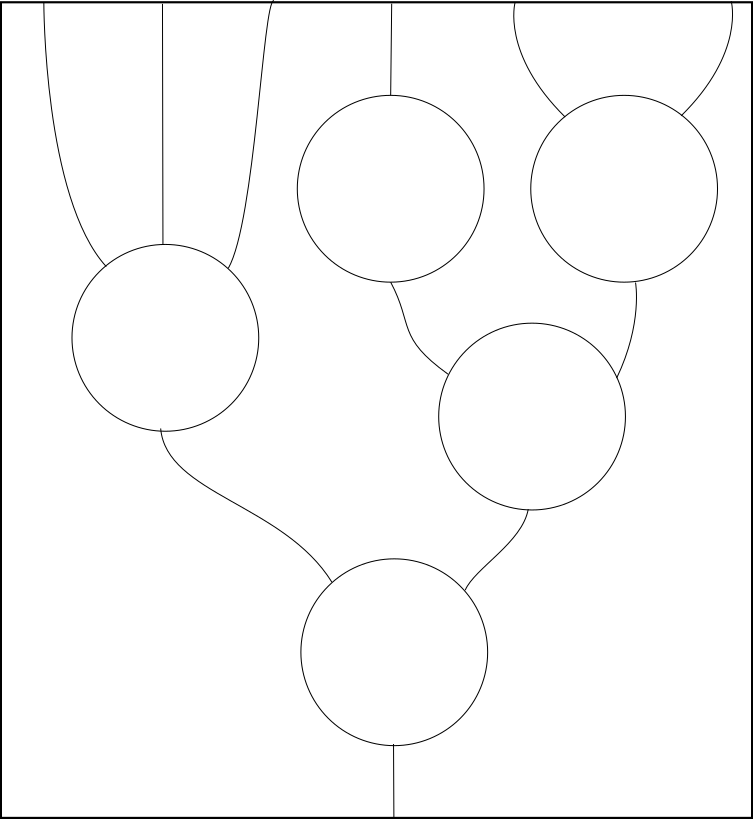
The composition rule then corresponds to taking the outputs of \(n\) \(k_i\)-ary operations and plugging them all into a single \(n\)-ary operation in order to generate a \(k_1 + \cdots + k_n\)-ary operation. For example, we might compose a ternary operator, a unary operator and a binary operator with another ternary operator to get a \(6\)-ary operator.
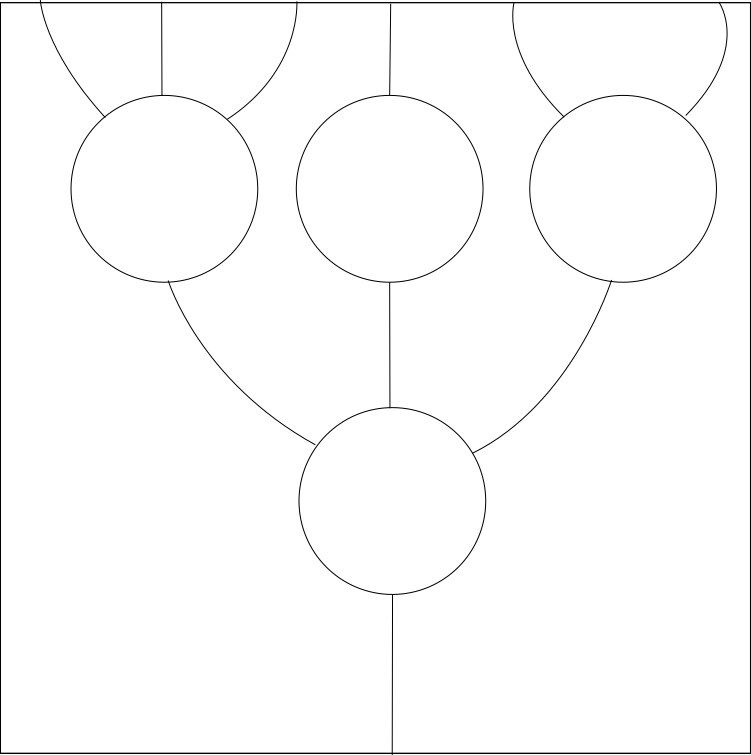
Our associativity rule then tells us that if we have three layers of operations, then we get the same result by composing the bottom two first that we do if we compose the top two first, so that it is well defined to draw a tree with three or more levels without specifying the order of composition.
Lastly, the identity rule gives us a single unary operation that is an identity for composition. This means that we can use it to ‘skip’ a level. Together with the associativity rule, this allows us to do away with the ‘level’ concept altogether when reasoning using string diagrams.
It’s important to remember that the elements of an operad are not in general themselves \(n\)-ary operators (as our sequences of real numbers example demonstrates), but that they admit operations very similar to those that are satisfied by real \(n\)-ary operators.
However, if \(A\) is a set and we set \([A^n,A]\) to be the set of all functions \(A^n \to A\) (in other words, actual \(n\)-ary operators on \(A\)), then the sets \([A^n,A]\) do naturally form an operad (via composition of functions) whose elements really are \(n\)-ary operators. Given an abstract operad \(O\), an algebra for \(O\) on a set \(A\) is defined to be an operad morphism \(O(-) \to [A^-,A]\); i.e., collection of functions \(O(n) \to [A^n,A]\) that commute with the composition and identity functions in the natural way. Essentially, this means that for each abstract ‘operator’ \(o\in O(n)\), we pick out an actual \(n\)-ary operator on \(A\) in such a way that the internal composition in \(O(-)\) corresponds to actual composition of functions (and likewise with the identity).
There is nothing particularly special about the category of sets, either. Any monoidal category \(\mathcal M\) admits a notion of \(n\)-ary operator: a morphism \(a \otimes \cdots \otimes a \to a\) for each object \(a\) of \(\mathcal M\). For a given \(a\), these sets of morphisms form an operad and we may define algebras for our operad \(O(-)\) on \(a\).
We’re getting somewhere. A little thought shows that if \(A\) is a set, then algebras for our operad \(C(-)\) on \(A\) correspond exactly to collections of binary operations \(\_+_s\_\) (for \(s\in[0,1]\)) that satisfy our original ‘associativity’ rule. Moreover, this definition extends very naturally on to any monoidal category.
Exercise
Show that there exists an operad whose algebras are monoids. (Work in the category of sets if you’re uncomfortable with monoids in arbitrary monoidal categories, but the operad you’ll come up with will work in that setting too.)
Symmetric operads
Having tackled the associativity rule, let’s move on to commutativity. It turns out that the operads in the previous section are not sufficient to describe this rule. One reason for that is as follows. We saw in the previous section that an operad admits a notion of algebra in any monoidal category. But it is not in general possible even to define the notion of commutativity in such a category, because we have no way to swap the order of variables. If we wanted to say that a binary operator \(\_+\_\colon A \times A \to A\) on a set \(A\) was commutative in the ordinary sense, for example, we could do this by asking that \(\_+\_\) was equal to the composite \((\_+\_) \circ \textrm{sym}\), where \(\textrm{sym}\colon A \times A \to A \times A\) swaps the pair around. But the monoidal product in an arbitrary monoidal category might not come equipped with such a ‘symmetry’ morphism.
We need a new type of operad to handle commutativity, and it’s called a symmetric, permutative or nonplanar operad (Actually, it’s more often called an operad, while the operads we met in the previous section are called nonpermutative or planar.) In this form of the operad, the wires that we use to join operations together are now allowed to cross.
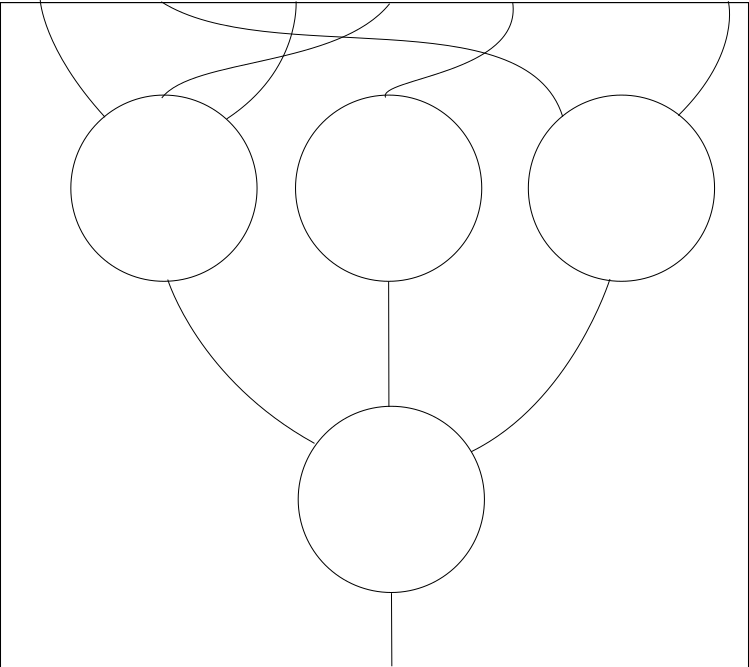
(This is where the name nonplanar comes from.) At the formal level, each set \(O(n)\) is now equipped with an action of the symmetric group \(\mathfrak S_n\). These actions are required to be compatible with the composition in a way that is rather tedious to write down, as it involves combining multiple permutations together to form a larger one. It’s a good exercise to try and write down the rules yourself.
In any case, our operad \(C(-)\) has this structure: given a sequence \(s_1,\cdots,s_n\) that sums to \(1\), we can apply a permutation \(\pi\in\mathfrak S_n\) to it to get the sequence
$$
s_{\pi(1)},\cdots,s_{\pi(n)}\,.
$$
Given a symmetric monoidal category, \(\mathcal S\), the collection of \(n\)-ary morphisms \(a \otimes \cdots \otimes a \to a\) forms a symmetric operad, and this gives us a notion of an algebra for a symmetric operad on any object of a symmetric monoidal category. The action of a permutation \(\pi \in \mathfrak S_n\) on \(O(n)\) is required to correspond to pre-composition with the natural symmetry \(a\otimes \cdots \otimes a \to a\otimes \cdots \otimes a\) corresponding to \(\pi\).
What does this mean for our operad \(C(-)\)? If we take \(\mathcal S\) to be the category of sets with Cartesian product, then it says that we must always have
$$
s_1a_1 + \cdots + s_na_n = s_{\pi(1)}a_{\pi(1)} + \cdots + s_{\pi(n)}a_{\pi(n)}
$$
for any permutation $\pi\in\mathfrak S_n$, which is precisely what the iterated version of our original ‘commutativity’ rule tells us. Therefore, algebras for \(C(-)\), now with its symmetric operad structure, on a set \(A\) correspond to families \(\_+_s\_\) of binary operations satisfying our associativity and commutativity rules.
Exercises
- Show that there exists a symmetric operad whose algebras are commutative monoids.
- Show that there exists a symmetric operad whose algebras (in a symmetric monoidal category) are (not necessarily commutative) monoids. This should be different from the planar operad of monoids that we met earlier.
Terminal operads
We have briefly touched on the definition of a morphism of operads, but let’s give it here explicitly. Given operads \(O’\) and \(O\), a morphism \(O’ \to O\) is given by functions \(\phi_n \colon O'(n) \to O(n)\) such that (writing operadic composition as \((\_,\cdots,\_);\_\)) we have
$$
\phi_{k_1+\cdots+k_n}((o_1,\cdots,o_n);p) = (\phi_{k_1}(o_1),\cdots\phi_{k_n}(o_n));\phi_n(p)
$$
for \(o_i\in O'(k_i), p\in O'(n)\), and
$$
\phi_1(e) = e\,,
$$
for \(e\) the identity element of each operad. A morphism of symmetric operads is a morphism between the underlying planar operads that also respects the actions of \(\mathfrak S_n\).
This makes operads (or symmetric operads) into a category. A terminal object of a category \(\mathcal C\) is an object \(()\) such that for any other object \(a\) of \(\mathcal C\), there is a unique morphism \(a \to ()\). For example, in the category of sets, the terminal objects are the one-element sets. There is a terminal object in the category of operads, given by a one-element set at each level. This is sometimes called \(\mathbf{Assoc}\), or the associative operad.
$$
\mathbf{Assoc}(n) = \{*\}
$$
This name comes from the fact that the algebras for this operad are objects with an associative (and unital) binary operation on them; i.e., monoids. If you have done the exercises then you will have come across it already. It is not difficult to see why this operad is terminal: given any other operad \(O\), there is a unique function \(O(n) \to {}\) for each \(n\), and the equation above is automatically satisfied, since both sides are functions into one-element sets, so are necessarily equal.
A consequence of this is that a monoid is automatically an algebra for any operad \(O\) that you can define. Indeed, we previously defined an algebra for an operad on an object \(s\) of a monoidal category to be an operad morphism into the operad
$$
[a^{\otimes n},a]
$$
given by morphisms \(a \otimes \cdots \otimes A \to a\).
That means that a monoid on \(a\) is given by an operad morphism
$$
\mathbf{Assoc} \to [a^{\otimes \_},a]\,.
$$
If \(O\) is another operad, then we have a unique operad morphism \(O \to \mathbf{Assoc}\), which we can compose with this morphism to give us the structure of an \(O\)-algebra on \(a\).
$$
O \to \mathbf{Assoc} \to [a^{\otimes \_},a]
$$
This is borne out by our operad \(C\) of sequences of reals summing to \(1\): given a monoid on a set \(M\) with binary operation \(*\), we can set \(a +_s b = a * b\) for all \(s\) and get something that satisfies the ‘associativity’ axiom that we gave for the operators \(\_+_s\_\). This shows that we were in some sense justified in using the word ‘associativity’ to describe that axiom.
The category of symmetric operads has a terminal object too. Once again, this is given by a singleton set at each level; the action of the symmetric groups is trivial. If you’ve done the exercise, you’ll know that the algebras for this symmetric operad are precisely the commutative monoids; hence, this is often called the commutative operad or \(\mathbf{Comm}\). You’ll also know that there is another symmetric operad whose algebras are not-necessarily commutative monoids (in a symmetric monoidal category). This is also called \(\mathbf{Assoc}\), since it represents the same algebraic theory, but is now given by
$$
\mathbf{Assoc}(n) = \mathfrak{S}_n\,,
$$
where the action of \(\mathfrak S_n\) is by composition of permutations. Since \(\mathbf{Comm}\) is terminal in the category of operads, we have a natural operad morphism \(\mathbf{Assoc} \to \mathbf{Comm}\), giving us a natural way to interpret any algebra for \(\mathbf{Comm}\) as an algebra for \(\mathbf{Assoc}\). This is not surprising, because:
Every commutative monoid is a monoid.
We can also link things to our operad \(C\) of sequences of reals. Given a commutative monoid with operation \(\_+\_\), we can set \(a +_s b = a + b\) for all \(s\) to get a model of both our ‘associativity’ and ‘commutativity’ axioms. This justifies our use of the word ‘commutativity’ to describe that axiom.
Cartesian Operads
Let’s get back to our operad of sequences of non-negative real numbers summing to \(1\). So far, we have managed to capture our original ‘associativity’ and ‘commutativity’ rules, but there are still two left – the ‘idempotence’ rule
$$
a +_t a = a
$$
and the rule for \(0\)
$$
a +_0 b = b\,.
$$
The operads we have met so far are not sufficient to capture these notions. To see why, let’s consider ordinary idempotence. Given a binary operation \(\_*\_\colon A \times A \to A\) on a set \(A\), we say that \(\_*\_\) is idempotent if the composite
$$
\require{AMSmath}
A \xrightarrow{\Delta} A \times A \xrightarrow{\_*\_} A
$$
is equal to the identity. Notice that we needed to bring in the diagonal map \(\Delta\) in order to make this definition. This is because in the defining equation for idempotence,
$$
a + a = a\,,
$$
the variable \(a\) is duplicated on the left hand side.
The operads we have met give us algebras in arbitrary symmetric monoidal categories. But not all symmetric monoidal categories admit a sensible morphism \(a \to a \otimes a\) to take on the role of the diagonal. Nor do they necessarily admit a morphism \(a \to I\) to allow us to forget variables. This means that since our ‘idempotence’ rule duplicates the variable \(a\) on the left, and since our zero rule forgets it on the right, neither of these rules makes sense in an arbitrary symmetric monoidal category. And so it wouldn’t make sense to try to find an operad to handle either of these equations.
In order to handle these rules, we need to extend our definition of an operad further. A Cartesian operad is like a symmetric operad, except that now each set \(O(n)\) admits an action not only of permutations \([n] \to [n]\), but of any function \(f\colon[n] \to [m]\). This means that such a function \(f\) gives rise to a function
$$
O(f) \colon O(n) \to O(m)\,.
$$
This assignment should make \(O\) into a functor; i.e., we should have \(O(g\circ f) = O(g)\circ O(f)\), and \(O(\textrm{id}) = \textrm{id}\). In addition, it should be compatible with the composition operator of the operad (I will leave it as an exercise to write down exactly what this means).
Sequences of non-negative real numbers that sum to \(1\) form a Cartesian operad. Indeed, given a function \(f \colon [n] \to [m]\) and a sequence \(a_1, \cdots, a_n\) of length \(n\) of non-negative real numbers that sum to \(1\), we can define a sequence of length \(m\), still summing to \(1\), given by
$$
(C(f)(a))_i = \sum_{p\in f^{-1}({i})} a_p\,.
$$
Now it is also possible to define a suitable notion of algebras for Cartesian operads. Given a Cartesian category \(\mathcal C\) (i.e., a monoidal category \(\mathcal C\) whose monoidal product is a category-theoretic Cartesian product) and an object \(A\) of \(\mathcal C\), we get a Cartesian operad
$$ [A^\_,A] $$
given at level \(n\) by the set of morphisms \(A^n \to A\), where the action of functions \(f \colon [n] \to [m]\) is given by pre-composition with the projection
$$ \langle \textrm{pr}_{f(1)}, \cdots, \textrm{pr}_{f(n)} \rangle \colon A^m \to A^n\,.
$$
This allows us to define an algebra for a Cartesian operad \(O\) on the object \(A\): it is an operad morphism \(O \to [A^\_, A]\) – in other words, a collection of actual operators \(A^n \to A\) replacing the abstract operators of the operad such that composition and function action in the operad correspond to composition of functions and pre-composition with projections as above. What do algebras for our operad \(C\) look like if we add in the Cartesian structure? To start with, since a morphism of Cartesian operads is in particular a morphism between the underlying symmetric operads, such an algebra must already satisfy all the rules we have put in place so far — namely, the associativity and commutativity rules. But now that we have to respect the Cartesian structure as well, we see that algebras for \(C\) with its Cartesian structure must in addition satisfy our idempotence and zero laws.
Indeed, suppose we have such an algebra on a set \(A\). Taking \(t\) to be the function \([2] \to [1]\) that sends both elements of \([2]\) to the unique element of \([1]\), we have the map
$$
C(t) \colon C([2]) \to C([1])
$$
sending the sequence \((s, 1-s)\) to the sequence \((1)\). Since \((1)\) is the operad identity, the operator \(+_s\) in the algebra must therefore satisfy
$$
a +_s a = a
$$
for all \(a \in A\).
Similarly, let \(c_2\) be the function \([1] \to [2]\) that sends \(1\) to \(2\). Then the function
$$
C(c_2) \colon C([1]) \to C([2])
$$
will send the unique unary length-\(1\) sequence \((1)\in C([1])\) to the length-\(2\) sequence \((0, 1)\). This means that we have
$$
b = a +_0 b
$$
for any \(a, b\in A\).
So at last we arrive at a possible alternative definition for the algebraic structures we started with: they are algebras for the Cartesian operad of finite sequences of real numbers summing to \(1\).
Lawvere Theories
A nice fact about Cartesian operads is that they are equivalent to things called Lawvere Theories (In fact, because they are equivalent, you can use either ‘Cartesian operad’ or ‘Lawvere theory’ to describe both concepts). To start with, Lawvere theories look quite different from the operads we have met so far. A Lawvere theory is defined to be a category \(\mathcal L\) whose objects are the natural numbers and which is such that for any \(m, n\), the object \(m + n\) is the category-theoretic product of \(m\) and \(n\). A morphism of Lawvere theories is defined to be a finite-product-preserving functor between categories.
I’ll stick to an informal description of how to get from a Cartesian operad to a Lawvere theory and vice versa, rather than giving a complete proof of equivalence. If we start with a Lawvere theory \(\mathcal L\), then we can define a Cartesian operad \(\bar{\mathcal L}\), where \(\bar{\mathcal L}(n)\) is the set of morphisms \(n \to 1\) in \(\mathcal L\). Given morphisms \(f_i \colon k_i \to 1\) for \(i = 1,\cdots,n\) and a morphism \(g \colon n \to 1\), the fact that \(k_1 + \cdots + k_n\) is the category theoretic product of the \(k_i\) and that \(n\) is the category-theoretic product of \(n\) copies of \(1\), allows us to compose these morphisms together into a morphism \((f_1,\cdots,f_n);g \colon k_1 + \cdots + k_n \to 1\). Given a function \(q \colon [m] \to [n]\), the action of \(q\) is precomposition with the morphism
$$ \langle \textrm{pr}_{q(1)}, \cdots, \textrm{pr}_{q(m)} \rangle \colon n = \underbrace{1 \times \cdots \times 1}_n \to \underbrace{1 \times \cdots \times 1}_m = m\,.
$$
In the other direction, suppose \(O\) is some Cartesian operad. Define the category \(\tilde{O}\) to have the natural numbers for objects and so that the morphisms \(m\to n\) are \(n\)-tuples of elements of \(O(m)\).
This means that we have \(\tilde O(k, m + n) \cong \tilde O(k, m) \times \tilde O(k, n)\), which is ultimately the reason why \(m+n\) is indeed the category-theoretic product of \(m\) and \(n\).
It remains to explain what composition of morphisms is in \(\tilde O\). Let \(m, n, k\) be natural numbers. Then we are looking for a way to take \(n\) elements of \(O(m)\) and \(k\) elements of \(O(n)\) and put them together to get \(n\) elements of \(O(m)\).
This doesn’t quite match up with our usual operadic notion of composition, which shouldn’t be a surprise, since the operadic composition in \(\bar{\mathcal L}\) didn’t line up with ordinary composition of morphisms in \(\mathcal L\). In order to define composition in \(\tilde O\), we need to imagine that we have \(m\) inputs that are shared between all \(n\) of our \(m\)-ary operators. Feeding these \(m\) inputs into each \(m\)-ary operator gives us \(n\) outputs, which we can then feed into each of the \(k\) \(n\)-ary operators in order to get \(k\) final outputs.
In symbols, let \(o_1,\cdots,o_n\in O(m)\) be a sequence of \(m\)-ary abstract operators and let \(p_1,\cdots,p_k\in O(n)\) be a sequence of \(k\)-ary abstract operators. for each \(j = 1, \cdots, k\), ordinary operadic composition would allow us to compose \(p_j\) with all of the \(o_i\) to get an \(mn\)-ary operator
$$
(o_1,\cdots,o_n);p_j \in O(mn)\,.
$$
We have a function \([mn] \to [m]\) that sends \(r\) to \(r \mathop{\textrm{mod}} n\) (in effect, dealing out the \(m\) inputs to each of the \(n\) \(m\)-ary operators). Applying the action, this now gives us our desired element of \(O(m)\).
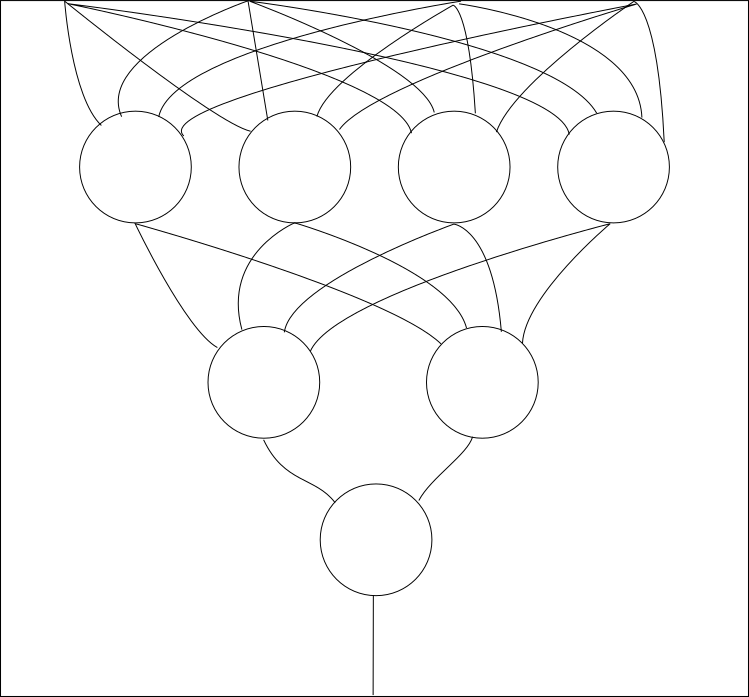
What happens if we apply this process to our Cartesian operad \(C\) of finite sequences of real numbers summing to \(1\)? Given \(m,n\), the set of morphisms \(m \to n\) is the set of \(n\)-tuples of length-\(m\) sequences that sum to \(1\); we will write the \(i\)-th element of the \(j\)-th sequence as \(a_{i,j}\).
Now suppose we have some such \(a_{i,j}\), for \(i=1,\cdots,m\) and \(j=1,\cdots,n\), and that we also have \(b_{j,k}\) for \(j=1,\cdots,n\) and \(k=1,\cdots,p\). How do we compose these together? Firstly, for each \(k\), we can form our usual operadic composition to yield the sequence
$$
a_{1,1}b_{1,k}, \cdots, a_{1,n}b{n,k},\cdots, a_{m,1}b_{1,k}, \cdots, a_{m,n}b_{n,k}\,.
$$
Now applying the ‘mod \(n\)’ function means collecting together all the terms \(a_{i,j}b_{j,k}\) for each \(j=1,\cdots,n\) and summing them together. We end up with the sequence given by
$$
(a;b)_{i,k} = \sum_{j=1}^n a_{i,j}b_{j,k}\,.
$$
That looks familiar – it’s the formula for matrix multiplication!
Everything becomes a bit easier once we’ve made that observation. We realize that the morphisms \(m \to n\) in our Lawvere theory can be thought of as \(m\times n\) real matrices whose rows sum to \(1\), otherwise known as \(m\times n\) stochastic matrices. Composition of morphisms is given by matrix multiplication, and we can verify that \(m+n\) is indeed the category theoretic product of \(m\) and \(n\) (if you like, identified with \(\mathbb R^{m+n}\), \(\mathbb R^m\) and \(\mathbb R^n\)), which comes down to the observations that the two projection matrices
$$ \left( \begin{array}{cccccc} 1 & & \mbox{$\Large{0}$} & & &\\ & \ddots & & & \mbox{$\Huge{0}$} & \\ \mbox{$\Large{0}$} & & 1 & & & \end{array} \right) \hspace{24pt} \left( \begin{array}{cccccc} & & & 1 & & \mbox{$\Large{0}$} \\ & \mbox{$\Huge{0}$} & & & \ddots & \\ & & & \mbox{$\Large{0}$} & & 1 \end{array} \right)$$
are stochastic and that a \(k\times (m+n)\) stochastic is uniquely the ‘pairing’ of a \(k\times m\) stochastic matrix \(A\) and a \(k\times n\) stochastic matrix \(B\):
$$
\begin{pmatrix}
\Huge A \\ \hline
\Huge B
\end{pmatrix}
$$
We end up with the following nice characterization of the algebraic structures we started with: they are algebras for the Lawvere theory of stochastic matrices.
Showing that an algebra for the stochastic matrix Lawvere theory satisfies the axioms we gave at the start boils down to showing a few matrix identities. For the associativity law, we start off with the two concrete ternary operators
$$
\begin{align} (a, b, c) & \mapsto a +_s b\\ (a, b, c) & \mapsto c\,.
\end{align} $$
Since an algebra for a Lawvere theory is a product-preserving functor into our ambient Cartesian category, we know that projection matrices must be sent to actual projections, so the second of these is described by the \(1\times 3\) projection matrix
$$
\begin{pmatrix} 0 & 0 & 1 \end{pmatrix}\,.
$$
The definition of the operator \(+_s\) is that it is the image of the \(1\times 2\) stochastic matrix \(\begin{pmatrix} s & 1-s \end{pmatrix}\). So the first operator corresponds to the matrix product
$$ \begin{pmatrix} s & 1-s \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix}= \begin{pmatrix} s & 1-s & 0 \end{pmatrix}\,. $$
We pair these two \(1\times 3\) matrices to give us the \(2\times 3\) matrix
$$
\begin{pmatrix} s & 1-s & 0 \\ 0 & 0 & 1\end{pmatrix}
$$
The interpretation of the operator corresponding to the expression \((a +_s b) +_t c\) now corresponds to multiplying this matrix by the \(1\times 2\) matrix \(\begin{pmatrix} t & 1-t \end{pmatrix}\), which gives us
$$ \begin{pmatrix}t & 1-t\end{pmatrix}\begin{pmatrix} s & 1-s & 0 \\ 0 & 0 & 1 \end{pmatrix}=\begin{pmatrix} st & (1-s)t & 1-t \end{pmatrix}\,. $$
Going in the opposite direction tells us that the operator corresponding to the expression \(a +_{s’} (b +_{t’} c)\) is given by the matrix
$$
\begin{pmatrix} s’ & (1-s’)t’ & (1-s’)(1-t’) \end{pmatrix}\,.
$$
If \(s\) and \(t\) are not both \(1\), we see that setting \(s’ = st\) and \(t’ = \frac{(1-s)t}{1-st}\) gives us equality between these two matrices. Whereas if \(s\) and \(t\) are both \(1\), then setting \(s’=1\) and letting \(t’\) be arbitrary will do.
Our remaining rules also correspond to various matrix identities. Our commutativity rule \(a +_s b = b +_{1-s} a\) corresponds to the fact that the matrix \(\begin{pmatrix} 1 – s & s \end{pmatrix}\) is what you get when you multiply \(\begin{pmatrix} s & 1-s \end{pmatrix}\) with the pairing of the projection on to the second factor with the projection on to the first factor (thus swapping the variables \(a\) and \(b\)).
$$
\begin{pmatrix} s & 1 – s \end{pmatrix} \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 – s & s \end{pmatrix}
$$
The idempotence rule \(a +_s a = a\) corresponds to the matrix identity
$$
\begin{pmatrix} s & 1-s \end{pmatrix} \begin{pmatrix} 1\\1 \end{pmatrix} = \begin{pmatrix} 1 \end{pmatrix}\,.
$$
Lastly, the zero rule corresponds to the fact that \(\begin{pmatrix} 0 & 1 \end{pmatrix}\) is projection on to the second factor.
None of these identities is particularly remarkable. The point is to show that we can condense and unify our original axioms using this stochastic matrix abstraction.
Checking the literature
So far, we have not actually proved that this new axiomatization via stochastic matrices is equivalent to what we started with. We have showed that any algebra for the Lawvere theory of stochastic matrices must in particular satisfy our four original axioms. But the possibility still remains that there are some equations, not implied by those original four, which nevertheless hold for all stochastic matrix algebras.
Proving that the two theories are in fact equivalent, while not particularly difficult, is not very enlightening. Fortunately, the work has been done for us. A quick online search for Lawvere theory of stochastic matrices turns up a paper by the mathematician Tobias Fritz, A presentation of the category of stochastic matrices [1]. Gratifyingly, that paper is like a reversed version of this blog post: it starts with the Lawvere theory of stochastic matrices (considered as a monoidal category) and tries to find a collection of axioms that generate the theory. The axioms he comes up with are the structural axioms for a Cartesian category, together with our original associativity, commutativity, idempotence and zero axioms.
Final thoughts
I hope this has been an enlightening introduction to the different types of operads, and to the idea that mathematical objects (in this case, finite sequences of real numbers summing to \(1\)) can sometimes be thought of as abstract operators. There are many directions we could go in from here. For example, there is a fairly simple monadic presentation of our axioms that we have not touched on, though it only works in the category of sets (In fact, all operads give rise to monads on the category of sets such that algebras for that monad are precisely the \(\mathbf{Set}\)-based algebras for the operad). Another area we have not explored is the topological structure of our operad. Sequences of reals of a fixed length (and, more generally, real-valued matrices) have a natural topological structure, under which the operads we have come up with are topological operads. In the Lawvere theory case, this says that the category in question is enriched over the category of topological spaces: indeed, stochastic matrices of fixed dimensions form a topological space, and matrix multiplication is continuous with respect to that topology. Useful real-world concepts of ‘interpolation’ should be continuous with respect to the interpolation constant and we’d need this topological structure in order to make that precise.
Many of the most interesting examples of operads come from geometric constructions. In Topological Quantum Field Theory, the symmetric operad of cobordisms (where an \(n\)-ary abstract operator is a diffeomorphism class of smooth manifolds with boundary whose boundary is made up of \(n\) negatively oriented circles together with one positively oriented circle. Given a suitable collection of these, we can glue them together along the boundaries in a way that almost exactly mirrors the string diagrams we have been using for illustration. It turns out that algebras for this operad can also be characterized by a simple equational theory [2], much as our stochastic matrix algebras could be characterized by our four axioms.
Conformal field theory involves a similar operad: this time, the abstract \(n\)-ary operators are Riemann spheres with \(n+1\) punctures, \(n\) negatively oriented and one positively oriented, with local coordinates vanishing at the punctures. By identifying punctures along the map \(z \mapsto 1/z\) via the local coordinates, we sometimes have a way to compose such spheres, in the operadic sense, to get a new punctured sphere. For technical reasons, this is not always possible, so what we really have is a partial operad: one where composition is not defined everywhere, but that satisfies the operad axioms where it is defined. A holomorphic algebra (i.e., an algebra in the category of complex vector spaces and holomorphic functions) for this operad is known as a vertex operator algebra [3], an important concept not only in quantum physics, but also in group theory and number theory. As in the topological case, Vertex Operator Algebras have a purely equational definition, but a notoriously complicated and unenlightening one. By contrast, the operadic definition gives us a concrete way to think about a vertex operator algebra: it gives us a way to introduce elements of a complex vector space at the negatively oriented punctures of a Riemann sphere and get a new element out at the positively oriented puncture, in a way that respects the gluing of punctured spheres that we have just introduced.
@misc{Fritz,
Author = {Tobias Fritz},
Title = {A presentation of the category of stochastic matrices},
Year = {2009},
Eprint = {arXiv:0902.2554},
}@misc{nlab:frobenius_algebra,
author = {{nLab authors}},
title = {{{F}}robenius algebra},
howpublished = {\url{http://ncatlab.org/nlab/show/Frobenius%20algebra}},
note = {\href{http://ncatlab.org/nlab/revision/Frobenius%20algebra/40}{Revision 40}},
month = may,
year = 2021
}[Bibtex]
@Inbook{Huang1993,
author="Huang, Yi-Zhi
and Lepowsky, James",
editor="Gelfand, Israel M.
and Corwin, Lawrence
and Lepowsky, James",
title="Vertex operator algebras and operads",
bookTitle="The {{G}}elfand Mathematical Seminars, 1990--1992",
year="1993",
publisher="Birkh{\"a}user Boston",
address="Boston, MA",
pages="145--161",
abstract="The notion of vertex operator algebra arose in the vertex operator construction of the Monster (see [FLM1], [B1] and [FLM2]). The algebraic theory of vertex operator algebras provides deep conceptual understanding of many (but not yet all) of the phenomena of monstrous moonshine (see [CN]) and at the same time establishes a solid foundation for the algebraic aspects of conformai field theory.",
isbn="978-1-4612-0345-2",
doi="10.1007/978-1-4612-0345-2_9",
url="https://doi.org/10.1007/978-1-4612-0345-2_9"
}